
True – The angles are corresponding angles on transversal s. Identifying Angles – Check for Understanding 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 False– The angles are adjacent angles on transversal r. < 3 and < 4 are alternate exterior angles. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators. Parallel Lines and Transversals Determine if the statement is true or false. Identifying Angles – Check for Understanding 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 < 3 and < 4 are alternate exterior angles. True – The angles are consecutive interior angles on transversal s. True – The angles are alternate interior angles on transversal q. Identifying Angles – Check for Understanding 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Determine if the statement is true or false. < 6 and < 12 are alternate interior angles. Key Points If the transversal cuts a pair of parallel lines, then the alternate interior angles are equal in measure. It is transversing both of these parallel lines. And this line that intersects both of these parallel lines, we call that a transversal. Well, actually, I'll do some points over here. So let me draw that line right over there. < 10 and < 11 are consecutive interior angles. Let me draw a little bit neater than that. < 6 and < 12 are alternate interior angles. < 10 and < 11 are consecutive interior angles. True - The angles are alternate exterior angles on transversal p. These lines will never intersect each other, however much we extend them to infinity. Select one of the options on the top left to. When two lines never cross each other, we call them parallel lines. False – The angles are vertical angles created by the intersection of q and r. The simulation shows two parallel lines, intersected by another line, called the transversal.

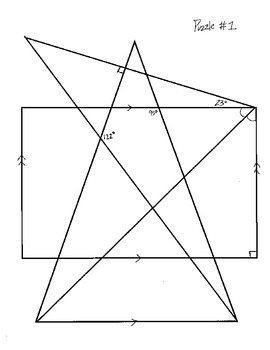

< 3 and < 5 are alternate interior angles. < 1 and < 15 are alternate exterior angles. The exterior angles are: Identifying Angles – Check for Understanding 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Determine if the statement is true or false. Parallel Lines and Transversals Identifying Angles - 1 2 3 4 5 6 7 8 Exterior angles are on the exterior of the two lines cut by the transversal. Answer: A transversal refers to a line which passes through two lines lying in the same plane at two different points. Therefore, line t is a transversal of lines j, k, and m. Lines j, k, and m are intersected by line t. The intersected lines do not have to be parallel. Parallel Lines and Transversals Transversal - A transversal is a line which intersects two or more lines in a plane. Parallel Lines and Transversals A slash through the parallel symbol || indicates the lines are not parallel. The symbol || is used to indicate parallel lines. Parallel Lines and Transversals What would you call two lines which do not intersect? Parallel A solid arrow placed on two lines of a diagram indicate the lines are parallel.


 0 kommentar(er)
0 kommentar(er)
