

Solve it using Matrix Method as an equation solver.Īnswer : Assume that x, y, and z are the three numbers. Rewrite the statement in form of the system of equations. The sum of the second and third when subtracted from the twice of first gives 1. The difference of thrice of first and five times the third gives 5. The sum of the two numbers and the twice of the second equals 2. Question 1: Suppose you have three numbers. Else, if (adj A) B = 0 then the system will either have infinitely many solutions (consistent system) or no solution (inconsistent system). If (adj A) B ≠ 0 (zero matrix), then the solution does not exist. If A is a singular matrix, then |A| = 0 then we calculate (adj A) B. This matrix equation provides a unique solution and is known as the Matrix Method.

Or, X = A – 1 B where, A – 1 = (adj A) ⁄ |A| Or, A – 1 (A X) = A – 1 B (pre-multiplying by A – 1)Īnd, I X = A – 1 B (I is the identity matrix) If A is a non-singular matrix i.e., |A| ≠ 0, then its inverse exists. The above system of equations can be represented in the form of a square matrix as We need to find the solution for the values of the variables in this system of equations.
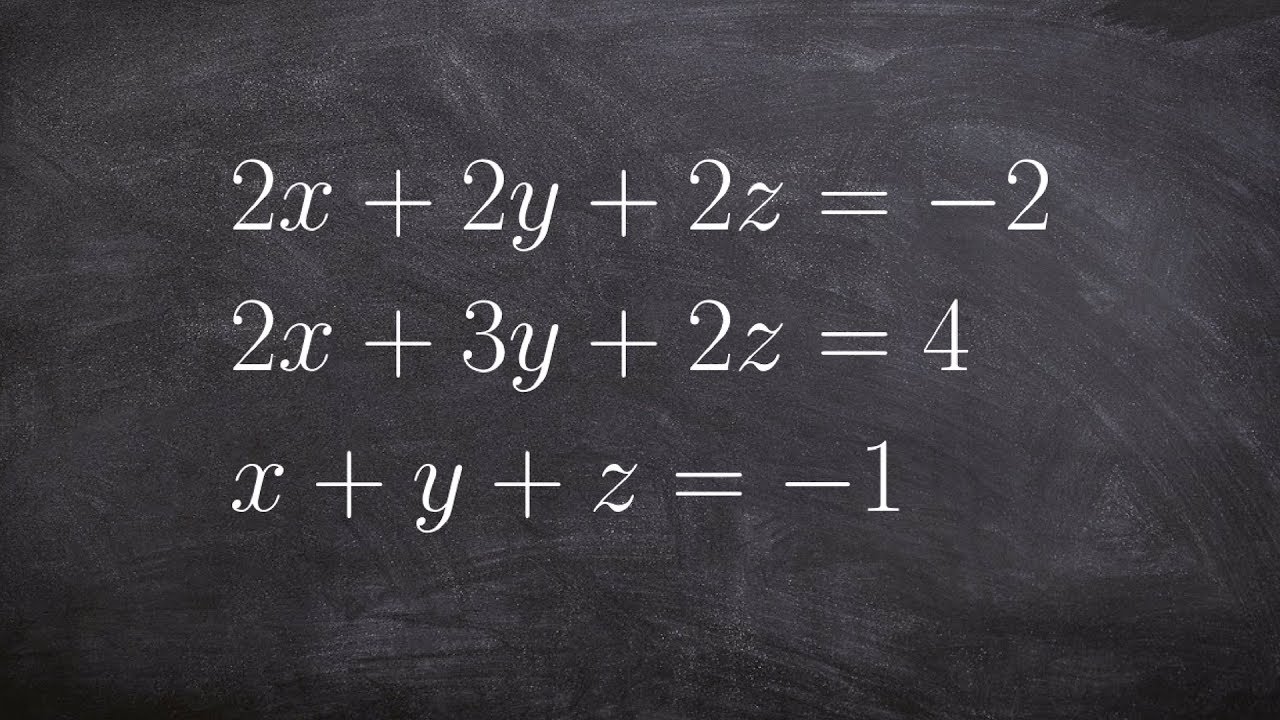
Where, x, y, and z are the variables and a 11, a 12, …, a 33 are the respective coefficients of the variables and b 1, b 2, and b 3 are the constants. Suppose we have the following system of equations The Solution of System of Linear EquationsĪ solution for a system of linear Equations can be found by using the inverse of a matrix. Inconsistent System: A system of equations with no solution is an inconsistent system.Consistent System: If one or more solution(s) exists for a system of equations then it is a consistent system.With the help of the determinant, we can also check for the consistency of linear equations. Here, we will discuss the way to solve a system of linear equations in two or three variables. Since now we are familiar with the way of calculating the determinant of a square matrix. ĭeterminants and Matrices as Equation Solver Then determinant of A is |A| = Δ = a 11 – a 12 + a 13. The number of rows is the same as the number of the columns in a square matrix. Substitute x = 2 into y = 3x – 8.A determinant of a square matrix of order n where a ij = (i, j) th element of A is a number (real or complex) associated with it. Then, substitute 3x – 8 for y into the equation 3x + 2y = 2. Isolate the variable y in the equation y + 8 = 3x to get y = 3x – 8. Then the expression is substituted in the other equation.įor example, to solve the system of equations
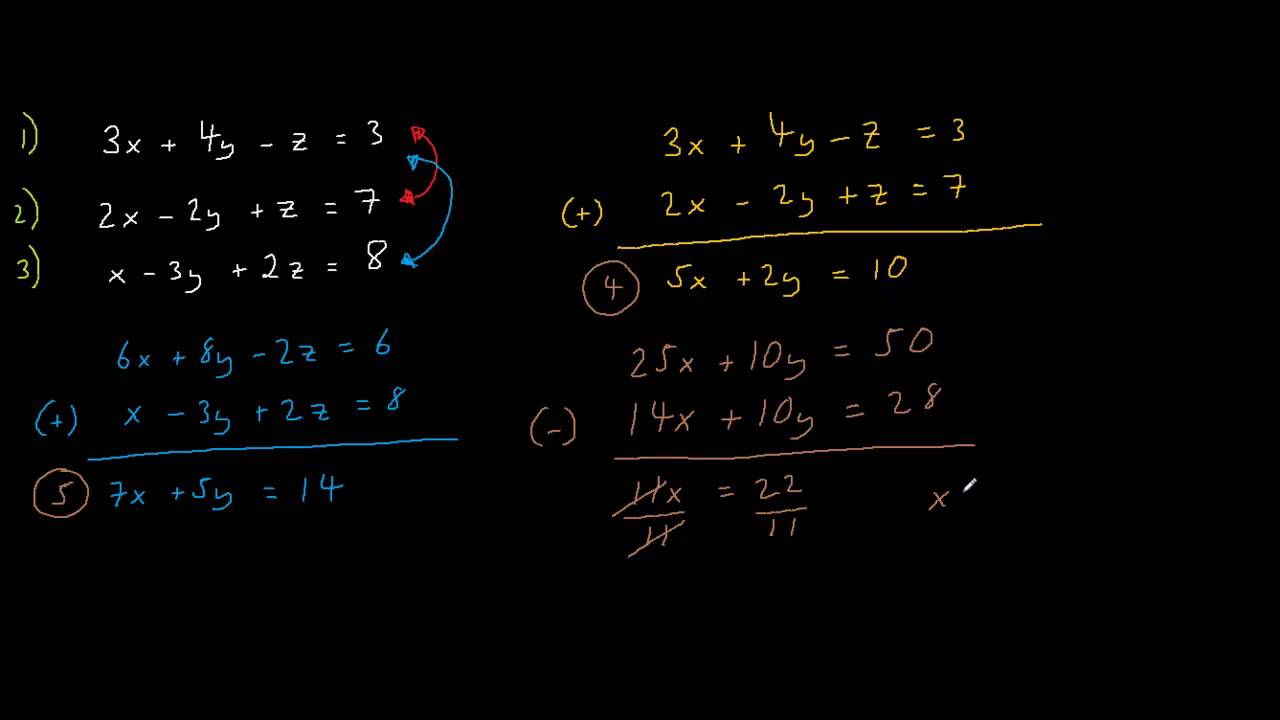
In the substitution method, one equation is manipulated to express one variable in terms of the other. There are two basic methods for solving systems of linear equations,īy substitution or by elimination. To solve a system of two equations means toįind an ordered pair of numbers that satisfies both equations in the system. System of equations, and the equations in the system are called Two equations with the same variables are called a If another linear equation in the same variables is given, it is usually possible to find a unique
Finding solutions for 3 equation systems with 2 variables how to#
Scroll down the page for more examples and solutions on how to solve systems of equations or simultaneous equations. The following diagram shows examples of how to solve systems of equations using substitution or elimination. Systems of Equations or Simultaneous Equations


 0 kommentar(er)
0 kommentar(er)
